No. 39 - Stacks Sharing an Array

Problem 1: How can you implement two stacks in a single array, where no stack overflows until no space left in the entire array space?

Analysis: An array has two ends, so each of the two stacks may grow from an end in the array. Figure 1 below shows the initial status of the array and two stacks (assuming the capacity of the array is 10).

Figure 1: Initial status of the array and two stacks

Since two stacks are empty at first, so indexes of top items are initialized as -1 and 10 at first.
When items are pushed into first stack, it grows from left to right. Similarly, the second stack grows from right to left when items are items are pushed into it. For example, Figure 2 shows the status when three items a, b and c are pushed into the first stack, and d, e are pushed into the second stack.

Figure 2: The status after three items are pushed into the first stack and two items are pushed into the second stack 

No more items can be pushed into stacks when two top items are adjacent to each other, because all space in the array has been occupied.

Our solution can be implemented with the following C++ class:

template <typename T, int capacity> class TwoStacks

{

public:

    TwoStacks()

    {

        topFirst = -1;

        topSecond = capacity;

    }

    T top(int stackIndex)

    {

        validateIndex(stackIndex);

        if(empty(stackIndex))

            throw new exception("The stack is empty.");

        if(stackIndex == 0)

            return items[topFirst];

        return items[topSecond];

    }

    void push(int stackIndex, T item)

    {

        validateIndex(stackIndex);

        if(full())

            throw new exception("All space has been occupied.");

        if(stackIndex == 0)

            items[++topFirst] = item;

        else

            items[--topSecond] = item;

    }

    void pop(int stackIndex)

    {

        validateIndex(stackIndex);

        if(empty(stackIndex))

            throw new exception("The stack is empty.");

        if(stackIndex == 0)

            --topFirst;

        else

            ++topSecond;

    }

    bool empty(int stackIndex)

    {

        if(stackIndex == 0 && topFirst == -1)

            return true;

        if(stackIndex == 1 && topSecond == capacity)

            return true;

        return false;

    }

private:

    bool full()

    {

        return (topFirst >= topSecond - 1);

    }

    void validateIndex(int stackIndex)

    {

        if(stackIndex < 0 || stackIndex > 1)

            throw new exception("Invalid Stack Index.");

    }

private:

    T items[capacity];

    int topFirst;

    int topSecond;

};

Problem 2: How can you implement n (n > 2) stacks in a single array, where no stack overflows until no space left in the entire array space?

Analysis: An array only has two ends, so we need new strategies to implement more than two stacks in a single array.

We may implement the array like a list, where each item in the array has a link to another item. When an item has not been occupied by any stacks and it is available, it is linked to the next available item. When an item is pushed into a stack, it is linked to the previous item in the stack. That’s to say, there are n + 1 list in total in the system if there are n stacks sharing an array, a list for the available space left in the array, and a list for each stack.

Let’s take three stacks sharing an array with capacity 10 as an example. Figure 3 shows the initial status for the array and stacks. Each item in the array has two blocks, one for item data and the other for the index of another block.

Figure 3: Initial status of three stacks sharing an array

As shown in Figure 3, each item is linked to the next item (the link block of the i^th item is i+1). The head of list for available items in the array points to the item at position 0, which is the Ava pointer in the figure. Since three stacks are empty, their top (Top1, Top2 and Top3 in the figure) are initialized as -1.

Let’s try to push an item a into the first stack. Currently the first available item is at the position 0, so we set its data block as a. The link block of the item is 1, which means the next available item is at the position 1, so we update the Ava pointer to the position 1. Additionally, the link block of the item at the position 1 should be updated to -1, the previous top index of the first stack. Lastly, we update to top index of the first stack to 0. The status of the array and stacks are shown in Figure 4.

Figure 4: The status after pushing a into the first stack

Let’s push two more items b and c into the first stack. The operations are similar as before, and the status is shown in Figure 5.

Figure 5: The status after adding two more items, b and c, into the first stack

In the next step we are going to push another d into the second stack. Most operations are similar as before. The link block in the item at the position 3 is updated to -1, since the second stack is empty before and its top index is -1 previously. And then the top index of the second stack is updated to 3. The status after adding d into the second stack is shown in Figure 6.

Figure 6: The status after pushing d into the second stack

If we continue to push three more item e, f, and g into the second stack, the status is shown in Figure 7.

Figure 7: The status after pushing three more items, e, f, and g, into the second stack

At this time we are going to pop an item from the first stack. Since the top index of the first stack is 2, the item to be popped off is at the position 2. The link value in that item is 1, which means the previous top in the first stack is at the position 1 in the array, so we update the top index of the first stack as 1. Now the item at the position 2 becomes available, it should be linked to the list for available items. We move the Ava pointer to 2, and then update the link value of the item at the position 2 as 7, which is the previous head position of the list for available items. The status is shown in Figure 8.

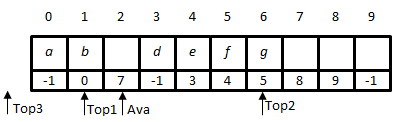Figure 8: The status after popping an item from the first stack

If we pop an item off the second stack, the item at the position 6 will be linked to the list for available items too. Figure 9 depicts the status after the related operations.

Figure 9: The status after popping an item off the second stack

If we push h into the third stack, it will be placed into the item at the position 6 because Ava points to that item. The next available item is at the position 2 (the link value in the item at the position 6). Therefore, the head of the list for available items points to location 2, as shown in Figure 10.

Figure 10: The status after pushing h into the third stack

Let’s continue to push four more items into the third stack, i, j, k, and l. The status after these four items are pushed is shown in Figure 11. At this time, there are two items in the first stack (a and b), three items in the second stack (d, e and f), and five items in the third stack (h, i, j, k, and l). Please note that items inside a stack are not necessarily adjacent. 

Figure 11: The status after pushing i, j, k, l into the third stack

After l is pushed into the item at the position 9, the Ava pointer is update to -1 (the previous link value in the item at the position 9), which means all items in the array have been occupied by stacks. We can’t push more items until some items are popped off.

The source code in C++ to implement stacks sharing an array is listed below:

template <typename T, int capacity, int count> class Stacks

{

public:

    Stacks()

    {

        int i;

        for(i = 0; i < capacity - 1; ++i)

            items[i].link = i + 1;

        items[i].link = -1;

        emptyHead = 0;

        for(i = 0; i < count; ++i)

            stackHead[i] = -1;

    }

    T top(int stackIndex)

    {

        validateIndex(stackIndex);

        if(empty(stackIndex))

            throw new exception("The stack is empty.");

        return items[stackHead[stackIndex]].data;

    }

    void push(int stackIndex, const T& item)

    {

        validateIndex(stackIndex);

        if(full())

            throw new exception("All space has been occupied.");

        Item<T>& block = items[emptyHead];

        int nextEmpty = block.link;

        block.data = item;

        block.link = stackHead[stackIndex];

        stackHead[stackIndex] = emptyHead;

        emptyHead = nextEmpty;

    }

    void pop(int stackIndex)

    {

        validateIndex(stackIndex);

        if(empty(stackIndex))

            throw new exception("The stack is empty.");

        Item<T>& block = items[stackHead[stackIndex]];

        int nextItem = block.link;

        block.link = emptyHead;
        emptyHead = stackHead[stackIndex];

        stackHead[stackIndex] = nextItem;

    }

    bool empty(int stackIndex)

    {

        return (stackHead[stackIndex] < 0);

    }

private:

    void validateIndex(int stackIndex)

    {

        if(stackIndex < 0 || stackIndex >= count)

            throw new exception("Invalid index of stack.");

    }

    bool full()

    {

        return (emptyHead < 0);

    }

private:

    template <typename T> struct Item

    {

        T data;

        int link;

    };

private:

    Item<T> items[capacity];

    int emptyHead;

    int stackHead[count];

};

More coding interview questions are discussed in my book <Coding Interviews: Questions, Analysis & Solutions>. You may find the details of this book on Amazon.com, or Apress.

The author Harry He owns all the rights of this post. If you are going to use part of or the whole of this ariticle in your blog or webpages, please add a reference to http://codercareer.blogspot.com/. If you are going to use it in your books, please contact him via zhedahht@gmail.com . Thanks.