Questions: Given an
array of ranges, please merge the overlapping ones. For example, four ranges
[5, 13], [27, 39], [8, 19], [31, 37] (in blue in Figure1) are merged into
two ranges, which are [5, 19] and [27, 39] (in green in Figure 1).
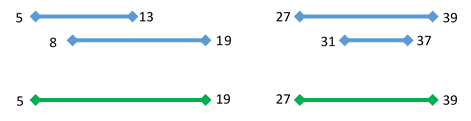 |
| Figure 1: Merge four ranges [5, 13], [27, 39], [8, 19] and [31, 37] (in blue), and get [5, 19], and [27, 39] (in green) |
Analysis: Before we
analyze how to merge an array of ranges, let’s discuss how to merge two ranges.
When two ranges don’t overlap each other, they can’t merge. When two ranges
overlap, the less starting value of two ranges becomes the starting value of
the merged range, and the greater ending value of two ranges becomes the ending
value of the merged range.
Therefore,
two ranges [5, 13] and [8, 19] are merged into a new range [5, 19], and two
ranges [27, 39] and [31, 37] are merged into a new range [27, 39]. The two
merged ranges can’t be merged further because they don’t overlap.
The
next question is: How to check whether two ranges overlap each other? When
two ranges overlap, there is at least on node in a range is contained in the
other range. For instance, the starting value 8 of the range [8, 19] is
contained in the range [5, 13], therefore, the two ranges [5, 13] and [8, 19]
overlap. No nodes in the range [8, 19] are contained in the range [31, 37], so
the two ranges don’t overlap.
The
following code shows how to merge two ranges, as well as to check whether two
ranges overlap:
public bool Contains(int value)
{
if (value >= this.Start && value <= this.End)
{
return true;
}
return false;
}
public bool Overlaps(Range other)
{
if (other == null)
{
return false;
}
if (this.Contains(other.Start) || this.Contains(other.End)
|| other.Contains(this.Start) || other.Contains(this.End))
{
return true;
}
return false;
}
public Range Merge(Range other)
{
if (!this.Overlaps(other))
{
throw new ApplicationException("Can't merge two
ranges.");
}
int newStart = (this.Start < other.Start) ? this.Start : other.Start;
int newEnd = (this.End > other.End) ? this.End : other.End;
return new Range(newStart, newEnd);
}
Now
let’s move on to merge an array of ranges.
The first step is to sort the ranges based on their start values. When
the ranges [5, 13], [27, 39], [8, 19], and [31, 37] are sorted, they are in the
order of [5, 13], [8, 19], [27, 39], and [31, 37].
The
next steps are to merge the sorted ranges. The merged ranges are inserted into
a data container. At each step, a range is retrieved from the sorted array, and
merged with the existing ranges in the container.
At
first the data container is empty, and the first range [5, 13] is inserted into
the container directly, without merging. Now there is only one range [5, 13] in
the container.
Then
the next range [8, 19] is retrieved. Since it overlaps the range[5, 13], and
they become [5, 19] when they merged. There is still only one range, which is [5,
19] in the container.
The
next range [27, 39] is retrieved, which does not overlap the range [5, 19] in
the container, so it is inserted into the range directly without merging. There
are two ranges [5, 19] and [27, 39] in the container.
The
last range in the sorted array is [31, 37]. It overlaps the last range [27, 39] in the container.
Therefore, the last range [27, 39] is deleted from the container, and then the
merged range is inserted into the container. At this step, the merged range is
also [27, 39].
Ranges
in the container are also sorted based on their starting values, and they don't
overlap each other. Notice that it's only necessary to check whether the new
range overlap the last range in the container. Why not the other ranges in the
container? Let's analyze what would happen when a new range in the sorted array
overlap two ranges in the container, with Figure 2:
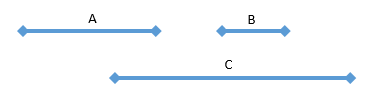 |
| Figure 2: It causes problems when a new range overlaps two ranges in the merged container |
In
Figure 2, the container has two ranges A and B, and a new range C is retrieved
from the sorted array, which overlaps the ranges A and B. Since C overlaps A,
the starting value of C should be less than the ending value of A. On the other
hand, C is retrieved from the sorted array later than B, the starting value of
C is greater than starting value of B. Additionally, B is behind A and they
don't overlap, so the starting value of B is greater than the ending value A.
Therefore, the starting value of C is greater than the ending value of A. It
contradicts.
Since
it's only necessary to merge new ranges from the sorted array with the last
range in the container. We implement the container as a stack, and the last
range is on the top of the stack.
The
following is the C# code to merge a sort an array of ranges:
public static Range[]
Merge(Range[] ranges)
{
Stack<Range> results = new Stack<Range>();
if (ranges != null)
{
Array.Sort(ranges, CompareRangeByStart);
foreach (var range in ranges)
{
if (results.Count == 0)
{
results.Push(range);
}
else
{
var top =
results.Peek();
if
(top.Overlaps(range))
{
var union = top.Merge(range);
results.Pop();
results.Push(union);
}
else
{
results.Push(range);
}
}
}
}
return results.Reverse().ToArray();
}
More coding interview questions are discussed
in my book< Coding Interviews: Questions, Analysis & Solutions>. You
may find the details of this book on Amazon.com,
or Apress.
The author Harry He
owns all the rights of this post. If you are going to use part of or the whole
of this ariticle in your blog or webpages, please add a reference to http://codercareer.blogspot.com/. If you are going to use it in your books,
please contact him via zhedahht@gmail.com . Thanks.




